now is better than never
[인공지능(AI) 기초 다지기] 4. 기초튼튼, 수학튼튼 (2) 본문
2) 딥러닝 학습방법 이해하기
- 신경망 (Neural Network)
- 선형 모델과 비선형 함수의 결합
- 데이터를 모아놓은 행렬 X, 행렬을 다른 벡터 공간으로 보내주는 가중치 행렬 W
두 개의 곱으로 선형모델 표현 - y절편을 표현한 행렬 b (각 행들이 전부 같은 값, 열 마다는 다를 수도 있음)


- 데이터가 바뀌면 결과값도 바뀜
출력 벡터의 차원은 d에서 p로 변화 - d 개의 변수로 p 개의 선형모델을 만들어 p 개의 잠재변수를 설명하는 모델
- W가 각각의 화살표를 의미
- Softmax 연산
- 선형회귀 -> Regression / 비선형 -> 분류(Classification)
- 소프트맥스 함수는 모델의 출력을 확률로 해석할 수 있게 변환해 주는 연산 (= 확률벡터로 변환)
- 분류문제를 풀 때 선형모델과 소프트맥스 함수를 결합하여 예측
- softmax(o) = softmax(Wx + b)
- 특정 벡터가 어떤 class에 속할 확률인지 계산 = 특정 클래스 k에 속할 확률
# softmax 함수 구현
def softmax(vec):
denumerator = np.exp(vec - np.max(vec, axis=1, keepdims=True) # exp : 지수함수, -max : overflow 방지
numerator = np.sum(denumerator, axis=1, keepdims=True)
val = denumerator / numerator
return val
def one_hot(val, dim):
return [np.eye(dim)[_] for _ in val]- 학습이 아닌 추론을 할 땐 소프트맥스 함수 사용 X
-> 원-핫(one-hot) 벡터로 최댓값을 가진 주소만 1로 출력하는 연산 사용
- 활성함수 (Activation Function)
- 신경망 = 선형모델 + 활성함수
- 소프트맥스는 출력물의 모든 값을 고려해서 연산
활성함수는 다른 주소의 출력값을 고려하지 않음, 벡터가 아닌 실수값만 input으로 받음 -> output도 실수 - 활성함수 σ는비선형함수로 잠재벡터 z = (z1,…,zq)의 각 노드에 개별적으로 적용하여 새로운 잠재벡터 H = (σ(z1), …, σ(zn))(히든벡터 = 뉴런 = 퍼셉트론)를 만듦
- 전통적으로는 시그모이드(sigmoid) 함수와 tanh 함수지만 오늘날 딥러닝에선 ReLU 함수를 많이 씀

- 신경망 수식

- z에 활성함수를 씌우면 새로운 잠재벡터인 H를 만들 수 있음
- 선형모델이 2개 쓰임 = 2-layer neural network
- 선형모델과 활성함수를 반복적으로 사용하는 것이 가장 기본적인 딥러닝모형
- x : input data point, o : output vector
- multi layer = 다층 신경망 퍼셉트론 (MLP) : 신경망이 여러층 합성된 함수
L개의 가중치 행렬 W와 y절편 b 를 parameter로 이루어져 있음 - forward propagation : L 까지의 순차적인 신경망 계산
- 층이 깊을 수록 목적함수를 근사하는데 필요한 뉴런(노드)의 숫자가 훨씬 빨리 줄어들어 좀 더 효율적인 학습 가능
= 층이 깊을 수록 적은 뉴런(노드))로 더 복잡한 패턴을 표현할 수 있음
= 층이 얇으면 필요한 뉴런의 숫자가 기하급수적으로 늘어나서 넓은(wide) 신경망이 되어야 함
=/ 그러나 최적화가 더 쉬운 것은 아님
- 역전파 알고리즘 (backpropagation)
- 경사하강법을 적용하여 각 층의 parameter의 미분을 계산하여 각각의 가중치 행렬들을 학습
- 역순으로 순차적으로 그래디언트 벡터 계산
- 저층의 그래디언트 벡터를 계산할 때 위층의 그래디언트 벡터가 필요함
- 연쇄법칙 : 합성함수의 미분법
- 역전파 알고리즘은 연쇄법칙(chain-rule) 기반 자동미분(auto-differentiation) 사용
- 각 노드의 텐서 값을 컴퓨터에 저장해야 미분 계산이 가능함
x에 대한 미분을 계산하고 싶을 경우 같이 사용된 x, y의 값을 알고 있어야 함

- 2층 신경망
- 히든 벡터 H는 입력 x로 부터 선형모델로 변형된 z 변수에 활성함수를 씌운 것
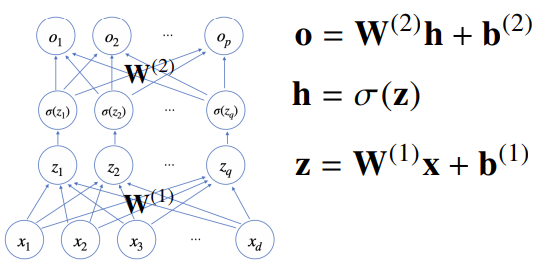
- W1에 경사하강법을 쓰고 싶을 경우?
각 성분에 대한 편미분을 구함 - 출력 o를 h로 미분 -> h를 다시 z로 미분 -> z를 다시 W1에 미분 을 순차적으로 곱함
'Python > [코칭스터디 9기] 인공지능 AI 기초 다지기' 카테고리의 다른 글
| [인공지능(AI) 기초 다지기] 5. 딥러닝 핵심 기초 (1) (0) | 2023.02.20 |
|---|---|
| [인공지능(AI) 기초 다지기] 4. 기초튼튼, 수학튼튼 (3) (0) | 2023.02.17 |
| [인공지능(AI) 기초 다지기] 4. 기초튼튼, 수학튼튼 (1) (0) | 2023.02.14 |
| [인공지능(AI) 기초 다지기] 3. 기초 수학 첫걸음 (4) (0) | 2023.02.09 |
| [인공지능(AI) 기초 다지기] 3. 기초 수학 첫걸음 (4) (0) | 2023.02.07 |

